Zarząd firmy DMUCHANE ATRAKCJE & ŻAK SWIM BARTŁOMIEJ ŻAK - BARTŁOMIEJ ŻAK, przedsiębiorca
BARTŁOMIEJ ŻAK, przedsiębiorca
Wiek firmy:
Wiek:
8 l. 2 mies. 22 d.
Działalność gospodarcza BARTŁOMIEJ ŻAK (CEIDG)
BARTŁOMIEJ ŻAK prowadzi jednoosobową działalność gospodarczą pod nazwą DMUCHANE ATRAKCJE & ŻAK SWIM BARTŁOMIEJ ŻAK, która jest zarejestrowana w Centralnej Ewidencji i Informacji o Działalności Gospodarczej (CEIDG). Firma działa od 2017-08-01 i ma swoją siedzibę pod adresem UL. JANA LECHONIA 539, PL-95-100, ZGIERZ. Główny zakres działalności BARTŁOMIEJ ŻAK to Działalność wesołych miasteczek i parków rozrywki (PKD główne: 93.21.Z). Pozostałe obszary działalności obejmują: wynajem i dzierżawa samochodów osobowych i lekkich pojazdów silnikowych, w tym motocykli, pozostała działalność usługowa, gdzie indziej niesklasyfikowana, działalność spa, saun i łaźni parowych, działalność usługowa związana z poprawą kondycji fizycznej, pozostała działalność rozrywkowa i rekreacyjna, gdzie indziej niesklasyfikowana i inne. NIP DMUCHANE ATRAKCJE & ŻAK SWIM BARTŁOMIEJ ŻAK: 7162693758. REGON DMUCHANE ATRAKCJE & ŻAK SWIM BARTŁOMIEJ ŻAK: 06039417900000.Znajdź inne firmy, w których w zarządzie znajduje się BARTŁOMIEJ ŻAK
Więcej informacji o DMUCHANE ATRAKCJE & ŻAK SWIM BARTŁOMIEJ ŻAK
Źródło informacji: Spółka Skarbu Państwa Centrum Rejestrów oraz dane przekazane przez firmę.
Informacje są niedokładne? Popraw je tutaj!
Wiadomości biznesowe, aktualności ekonomiczne, artykuły
Inne wiadomości
Oby Nagroda Sacharowa dla Andrzeja Poczobuta przyspieszyła jego zwolnienie
Andrzej Poczobut jako krytyk reżimu Aleksandra Łukaszenki stał się symbolem walki Białorusinów o wolność i demokrację.
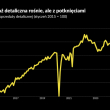
Dane o sprzedaży detalicznej przykrywają wstrzemięźliwość konsumenta
We wrześniu sprzedaż w sklepach wyskoczyła w górę aż o 6,4 proc. w porównaniu z poprzednim rokiem. Jednak te dane nie mówią całej prawdy o konsumentach. Pod powierzchnią widać ostrożność w zakupach
Fabryka w Nowym Tomyślu podwoi moce niemieckiej Josery
Erbacher uruchomił w Polsce zakład produkujący karmę dla zwierząt domowych, który ma stać się jednym z głównych filarów grupy.